Ahmed’s integral

The special case $a=1$ in the following problem is known as Ahmed’s integral. I have no idea why the integral proposed by Zafar Ahmed became so ridiculously popular; there are many integrals which are much harder and nicer yet never as popular as this integral. Anyway, here it is.

Problem. Show that

$\displaystyle \begin{aligned}I(a):=\int_0^1 \frac{\arctan \sqrt{x^2+2a^2}}{(x^2+a^2)\sqrt{x^2+2a^2}} \ dx = \frac{\pi \arctan\left(\frac{1}{\sqrt{2a^2+1}}\right)-\left(\arctan\left(\frac{1}{a}\right)\right)^2}{2a^2}, \ \ \ \ \ \ \ a \ne 0.\end{aligned}$

Solution. We have

$\displaystyle \begin{aligned}I(a)=\int_0^1 \frac{\frac{\pi}{2}-\arctan\left(\frac{1}{\sqrt{x^2+2a^2}}\right)}{(x^2+a^2)\sqrt{x^2+2a^2}} \ dx = \frac{\pi}{2}\int_0^1\frac{dx}{(x^2+a^2)\sqrt{x^2+2a^2}} \ dx - J(a),\end{aligned} \ \ \ \ \ \ \ \ (1)$

where

$\displaystyle J(a):=\int_0^1 \frac{\arctan\left(\frac{1}{\sqrt{x^2+2a^2}}\right)}{(x^2+a^2)\sqrt{x^2+2a^2}} \ dx.$

It is easy to see that

$\displaystyle \begin{aligned}\int_0^1\frac{dx}{(x^2+a^2)\sqrt{x^2+2a^2}} \ dx=\left[\frac{\arctan\left(\frac{x}{\sqrt{x^2+2a^2}}\right)}{a^2}\right]_{x=0}^{x=1} =\frac{\arctan\left(\frac{1}{\sqrt{2a^2+1}}\right)}{a^2}.\end{aligned} \ \ \ \ \ \ \ \ (2)$

We also have

$\displaystyle \begin{aligned}J(a)=\int_0^1\frac{\sqrt{x^2+2a^2}}{(x^2+a^2)\sqrt{x^2+2a^2}}\int_0^1\frac{dy}{y^2+x^2+2a^2} \ dx=\int_0^1\frac{1}{x^2+a^2}\int_0^1\frac{dy}{y^2+x^2+2a^2} \ dx \end{aligned}$

$\displaystyle \begin{aligned}=\int_0^1 \int_0^1 \frac{dx}{(x^2+a^2)(x^2+y^2+2a^2)} \ dy=\int_0^1 \frac{1}{y^2+a^2}\int_0^1\left(\frac{1}{x^2+a^2}-\frac{1}{x^2+y^2+2a^2}\right)dx \ dy \end{aligned}$

$\displaystyle \begin{aligned}=\left(\int_0^1 \frac{dx}{x^2+a^2}\right)^2 - \int_0^1 \frac{1}{y^2+a^2} \int_0^1\frac{dx}{x^2+y^2+2a^2} \ dy=\left(\int_0^1 \frac{dx}{x^2+a^2}\right)^2-\int_0^1 \frac{\arctan\left(\frac{1}{\sqrt{y^2+2a^2}}\right)}{(y^2+a^2)\sqrt{y^2+2a^2}} \ dy\end{aligned}$

$\displaystyle =\left(\frac{\arctan\left(\frac{1}{a}\right)}{a}\right)^2 - J(a),$

which gives

$\displaystyle J(a)=\frac{1}{2}\left(\frac{\arctan\left(\frac{1}{a}\right)}{a}\right)^2. \ \ \ \ \ \ \ \ (3)$

The result now follows from $(1),(2),(3). \ \Box$

Exercise. Prove the identity $(2).$

Fractional part integrals (4)

This problem was asked on the Art of Problem Solving recently; here you can see the problem and my solution. I’m going to repost my solution here but in a slightly better way.

Problem. Let $k > 0$ be a real number, and let $\{x\}, \lfloor x \rfloor$ be, respectively, the fractional and the integer part of a real number $x.$ Let $H_r, \ r > -1,$ be the harmonic number defined in this post. Show that

i) $\displaystyle \int_0^1\frac{\{1/x\}^k}{x+1} \ dx = \int_0^1\frac{x^k}{x+1} \ dx=\frac{1}{2}\left(H_{\frac{k}{2}}-H_{\frac{k-1}{2}}\right)$

ii) $\displaystyle \int_0^1 \int_0^1 \left\{\frac{x}{1-xy}\right\}^k dx \ dy=\int_0^1 \left\{\frac{1}{x}\right\}^k dx.$

Solution. i) We begin with the substitution $x=1/t.$ Then

$\displaystyle \int_0^1\frac{\{1/x\}^k}{x+1} \ dx=\int_1^{\infty}\frac{\{t\}^k}{t(t+1)} \ dt=\int_1^{\infty}\frac{(t-\lfloor t \rfloor)^k}{t(t+1)} \ dt=\sum_{n \ge 1}\int_n^{n+1}\frac{(t-\lfloor t \rfloor)^k}{t(t+1)} \ dt$

$\displaystyle =\sum_{n \ge 1}\int_n^{n+1}\frac{(t-n)^k}{t(t+1)} \ dt =\sum_{n \ge 1}\int_0^1\frac{t^k}{(t+n)(t+n+1)} \ dt=\int_0^1t^k\underbrace{\sum_{n \ge 1}\left(\frac{1}{t+n}-\frac{1}{t+n+1}\right)}_{\text{telescoping series}} dt$

$\displaystyle =\int_0^1\frac{t^k}{t+1} \ dt=\frac{1}{2}\left(H_{\frac{k}{2}}-H_{\frac{k-1}{2}}\right).$

The last identity holds by Exercise 8, iv), in this post.

ii) Let

$\displaystyle I:=\int_0^1 \int_0^1 \left\{\frac{x}{1-xy}\right\}^k dx \ dy, \ \ \ \ \frac{x}{1-xy}=\frac{1}{t}.$

Then

$\displaystyle I=\int_0^1 \int_{1-y}^{\infty}\frac{\{1/t\}^k}{(t+y)^2} \ dt \ dy=\int_0^1\{1/t\}^k\int_{1-t}^1\frac{dy}{(t+y)^2} \ dt + \int_1^{\infty}\{1/t\}^k\int_0^1\frac{dy}{(t+y)^2} \ dt$

$\displaystyle \begin{aligned}=\int_0^1\frac{t\{1/t\}^k}{t+1} \ dt + \int_1^{\infty}\frac{\{1/t\}^k}{t(t+1)} \ dt=\int_0^1 \{1/t\}^k dt -\int_0^1\frac{\{1/t\}^k}{t+1} \ dt + \int_1^{\infty}\frac{\{1/t\}^k}{t(t+1)} \ dt\end{aligned}$

$\displaystyle =\int_0^1 \{1/t\}^k dt -\int_0^1\frac{\{1/t\}^k}{t+1} \ dt + \int_0^1\frac{\{s\}^k}{s+1} \ ds, \ \ \ \ \ \ s=1/t$

$\displaystyle \begin{aligned}=\int_0^1 \{1/t\}^k dt -\int_0^1\frac{\{1/t\}^k}{t+1} \ dt + \int_0^1\frac{s^k}{s+1} \ ds, \ \ \ \ \ \ \text{because} \ s=\{s\} \ \text{for} \ s \in [0,1)\end{aligned}$

$\displaystyle = \int_0^1 \{1/t\}^k dt -\int_0^1\frac{t^k}{t+1} \ dt + \int_0^1\frac{s^k}{s+1} \ ds, \ \ \ \ \ \ \ \text{by i)}$

$\displaystyle =\int_0^1 \{1/t\}^k dt. \ \Box$

Remark. For the integrals of the form $\displaystyle \int_0^1\{1/x\}^kdx,$ where $k$ is a positive integer, see this post.

Exercise. Show that

$\displaystyle \int_0^1\frac{\sqrt{\{1/x\}}}{x+1} \ dx=2-\frac{\pi}{2}.$

Convergence of the sequence {x_n} defined by x_{n+1} = x_n + (x_n/n)^2

The following problem was asked in the Art of Problem Solving forum; here you can see the question (post #4) and my answer (post #5).

Remark. In steps 2), 4), and 5) of the solution of the following Problem, we have used this fact that any bounded sequence of real numbers that is either increasing or decreasing, is convergent (see the Fact in this post!).

Problem. Consider the sequence 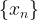$\{x_n\}$ defined by

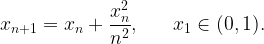
$\displaystyle x_{n+1}=x_n+\frac{x_n^2}{n^2}, \ \ \ \ \ x_1 \in (0,1).$

Show that 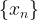$\{x_n\}$ is convergent.

Solution. I’m going to give the solution in several steps.

1) The sequence $\displaystyle \frac{x_n}{n}$ is decreasing.

Proof. It’s clear that $x_n > 0$ and, by induction, $x_n < n.$ Thus

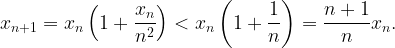
$\displaystyle x_{n+1}=x_n\left(1+\frac{x_n}{n^2}\right) < x_n\left(1+\frac{1}{n}\right)=\frac{n+1}{n}x_n.$

2) $\displaystyle a:=\lim_{n\to\infty}\frac{x_n}{n}=0.$

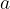Proof. By 1), $\displaystyle 0 < \frac{x_n}{n} \le x_1 < 1$ and so $a$ exists and 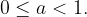$0 \le a < 1.$ Now, by Stolz-Cesaro,

$\displaystyle a=\lim_{n\to\infty}(x_{n+1}-x_n)=\lim_{n\to\infty}\frac{x_n^2}{n^2}=a^2$

and so $a=0.$

3) The sequence $\displaystyle \frac{x_n}{\sqrt[3]{n}}$ is eventually decreasing.

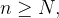Proof. By 2), there exists an $N$ such that $\displaystyle x_n < \frac{n}{4}$ for all $n \ge N.$ It is easy to see that $\displaystyle \frac{\sqrt[3]{1+x}-1}{x} > \frac{1}{4}$ for all $0 < x \le 1$ and so, for $n \ge N,$ we have

$\displaystyle x_n < \frac{n}{4} < n^2\left(\sqrt[3]{1+\frac{1}{n}}-1\right),$

which then gives

$\displaystyle \frac{x_{n+1}}{\sqrt[3]{n+1}}=\frac{x_n}{\sqrt[3]{n+1}}+\frac{x_n^2}{n^2\sqrt[3]{n+1}} < \frac{x_n}{\sqrt[3]{n}}.$

4) $\displaystyle b:=\lim_{n\to\infty}\frac{x_n}{\sqrt[3]{n}}=0.$

Proof. By 3), 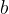$b$ exists (as a finite number), and so, by Stolz-Cesaro,

$\displaystyle b=\lim_{n\to\infty}\frac{x_{n+1}-x_n}{\sqrt[3]{n+1}-\sqrt[3]{n}}=\lim_{n\to\infty}\frac{x_n^2}{n^2(\sqrt[3]{n+1}-\sqrt[3]{n})}=3\lim_{n\to\infty}\frac{\sqrt[3]{n^2}x_n^2}{n^2}$

$\displaystyle =3\lim_{n\to\infty}\frac{x_n^2}{n\sqrt[3]{n}}=3 b\lim_{n\to\infty}\frac{x_n}{n}=0, \ \ \ \ \ \ \ \text{by 2)}.$

5) The sequence 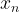$x_n$ is convergent.

Proof. By 4), there exists an $N$ such that $x_n < \sqrt[3]{n}$ for all $n \ge N$ and so

$\displaystyle x_{n+1}-x_n=\frac{x_n^2}{n^2} < \frac{\sqrt[3]{n^2}}{n^2}=\frac{1}{n\sqrt[3]{n}}.$

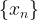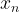Hence $\{x_n\}$ is bounded, because the series $\sum \frac{1}{n\sqrt[3]{n}}$ converges, and so the sequence $x_n$ converges because it is increasing. $\Box$

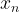Exercise. Regarding step 5) of the solution, explain why the fact that the series $\sum \frac{1}{n\sqrt[3]{n}}$ converges implies that the sequence $x_n$ is bounded.

A basic application of basic calculus in basic number theory

Higher calculus, i.e. complex analysis, has many important applications in higher number theory. How about applications of basic calculus in basic number theory, do we have nice examples of that? Sure we do, here is one.

Let $d,n \ge 2$ be integers. It is clear that if $d \mid n,$ then $d^k \mid n^m$ for all positive integers $m \ge k.$ The converse is also true if $m=k,$ i.e. if $d^k \mid n^k,$ then clearly $d \mid n.$ But if $m > k,$ the converse is not necessarily true, e.g. $d=8, \ n=4, \ k=2, \ m=3.$ In fact, for any integer $k \ge 2,$ there exist integers $d,n \ge 2$ such that

$d^2 \mid n^3, \ d^3 \mid n^4, \cdots , d^k \mid n^{k+1}, \ \ d \nmid n,$

for example, choose $d=a^{k+1}, \ n=a^k,$ where $a \ge 2$ is any integer. What if $k=\infty$ ? That is, can we have $d^2 \mid n^3, \ d^3 \mid n^4, \cdots ,$ and yet $d \nmid n$ ? The answer is no, and here’s one way to prove it. Let $p$ be a prime divisor of $d$ and let $r,s$ be the exponents of $p$ in the prime factorizations of $d, n,$ respectively. Since we are assuming that $d^j \mid n^{j+1},$ for all integers $j \ge 2,$ we have $rj \le s(j+1)$ and so $\displaystyle \frac{r}{s} \le \frac{j+1}{j}.$ Taking limit as $j \to \infty$ gives $\displaystyle \frac{r}{s} \le 1$ and so $r \le s,$ proving that $d \mid n.$

The Riemann zeta function; evaluating ζ(2n)

Here we defined the Riemann zeta function $\zeta(\alpha), \ 1 < \alpha \in \mathbb{R},$ as the infinite series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{\alpha}}$ and here we proved that $\displaystyle \zeta(2)=\frac{\pi^2}{6}.$ In this post, we find $\zeta(2n)$ for all positive integers $n.$

Theorem. Let $\{B_n\}$ be the sequence of Bernoulli numbers. Then

$\displaystyle \zeta(2n)=(-1)^{n-1}\frac{2^{2n-1}B_{2n}\pi^{2n}}{(2n)!},$

for all positive integers $n.$

Proof. The idea of the proof is both clever and simple: find the Taylor series expansion of the function $\displaystyle \frac{x}{\sinh x}$ in a neighborhood of $x=0$ in two ways and then equate the coefficients of $x^n$ in the two series to get the desired formula.

First Way. We have for all $x \in \mathbb{R},$

$\displaystyle \begin{aligned}\frac{x}{\sinh x}=\frac{2x}{e^x-e^{-x}}=\frac{2xe^x}{e^{2x}-1}=\frac{2x(e^x+1-1)}{e^{2x}-1}=\frac{2x}{e^x-1}-\frac{2x}{e^{2x}-1}\end{aligned}$

$\displaystyle \begin{aligned}=2\sum_{n=0}^{\infty}\frac{B_n}{n!}x^n-\sum_{n=0}^{\infty}\frac{B_n}{n!}(2x)^n=\sum_{n=0}^{\infty}\frac{(2-2^n)B_n}{n!}=1+\sum_{n=1}^{\infty}\frac{(2-2^{2n})B_{2n}}{(2n)!}x^{2n},\end{aligned} \ \ \ \ \ \ \ \ (1)$

because $B_0=1, \ B_{2n+1}=0, \ n \ge 1.$

Second Way. By Problem 2 in this post,

$\displaystyle \frac{\pi a}{\sinh(\pi a)}=1-2a^2\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k^2+a^2}, \ \ \ \ \ \ a \in \mathbb{R},$

and so letting $\pi a=x$ and assuming $|x| < \pi,$ we have

$\displaystyle \frac{x}{\sinh x}=1-\frac{2x^2}{\pi^2}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k^2+\frac{x^2}{\pi^2}}=1-\frac{2x^2}{\pi^2}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k^2} \cdot \frac{1}{1+\frac{x^2}{k^2\pi^2}}$

$\displaystyle =1-\frac{2x^2}{\pi^2}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k^2}\sum_{n=0}^{\infty}(-1)^n\left(\frac{x^2}{k^2\pi^2}\right)^n=1-2\sum_{k=1}^{\infty}(-1)^{k-1}\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n+2}}{k^{2n+2}\pi^{2n+2}}$

$\displaystyle =1-2\sum_{k=1}^{\infty}(-1)^{k-1}\sum_{n=1}^{\infty}(-1)^{n-1}\frac{x^{2n}}{k^{2n}\pi^{2n}}=1-2\sum_{n=1}^{\infty}(-1)^{n-1}\frac{x^{2n}}{\pi^{2n}}\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k^{2n}}$

$\displaystyle =1-2\sum_{n=1}^{\infty}(-1)^{n-1}\frac{(1-2^{1-2n})\zeta(2n)}{\pi^{2n}}x^{2n},$

where the last identity is just the second identity in Problem 1, i), in this post. So we have shown that for $|x| < \pi,$

$\displaystyle \frac{x}{\sinh x}=1-2\sum_{n=1}^{\infty}(-1)^{n-1}\frac{(1-2^{1-2n})\zeta(2n)}{\pi^{2n}}x^{2n}. \ \ \ \ \ \ \ \ \ (2)$

Now, equating the coefficients of $x^{2n}$ in $(1), (2)$ gives

$\displaystyle \frac{(2-2^{2n})B_{2n}}{(2n)!}=-2(-1)^{n-1}\frac{(1-2^{1-2n})\zeta(2n)}{\pi^{2n}}$

and the result follows. $\ \Box$

Example. Since $\displaystyle B_2=\frac{1}{6}, \ B_4=-\frac{1}{30},$ we have by the theorem,

$\displaystyle \begin{aligned} \sum_{n=1}^{\infty} \frac{1}{n^2}=\zeta(2)=\frac{2B_2\pi^2}{2!}=\frac{\pi^2}{6}, \ \ \ \ \ \ \sum_{n=1}^{\infty} \frac{1}{n^4}=\zeta(4)=-\frac{8B_4\pi^4}{4!}=\frac{\pi^4}{90}.\end{aligned}$

Exercise 1. Show that $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^6}=\frac{\pi^6}{945}.$

Exercise 2. In the proof of the Theorem, the Second Way, why did we need the condition $|x| < \pi$ ?

Exercise 3. Show that $\displaystyle \frac{(2n-1)!(4^n-1)\zeta(2n)}{\pi^{2n}}$ is an integer for any integer $n \ge 2.$
Hint. See this post!

Exercise 4. Show that

$\displaystyle \lim_{n\to\infty}\frac{(-1)^nB_{2n}}{\sqrt{n}}\left(\frac{\pi e}{n}\right)^{2n}=-4\sqrt{\pi}.$

Hint. First use the above Theorem, then Stirling’s formula, and finally Problem 1, iii), in this post.

Using the Lambert W-function (1)

Here we used the beautiful and mysterious Lambert W-function to solve some equations but the problem with those examples and many other examples of that kind is that the appearance of the Lambert function was expected from the beginning, which makes the examples not interesting.

In this post, I’m going to give an example where the Lambert W-function appears unexpectedly and solves the problem! I should thank the user who posted the problem on the Art of Problem Solving website.

Problem (American Mathematical Monthly). Show that

$\displaystyle \sum_{k=0}^n(-1)^k\binom{n}{k}(k+1)^{k-1}k^{n-k}=(-1)^n,$

for all integers $n \ge 0.$ As always, we define $0^0:=1.$

Solution (Y. Sharifi). Let

$\displaystyle a_n:=\sum_{k=0}^n(-1)^{n-k}\binom{n}{k}(k+1)^{k-1}k^{n-k}, \ \ \ \ \ \ n \ge 0,$

and consider the function

$\displaystyle f(x):=\sum_{n \ge 0}\frac{a_n}{n!}x^n, \ \ \ \ \ \ \ 0 < x < 1.$

We have

$\displaystyle f(x)=\sum_{n \ge 0} \sum_{k=0}^n\frac{(-1)^{n-k}\binom{n}{k}(k+1)^{k-1}k^{n-k}}{n!}x^n=\sum_{n \ge 0} \sum_{k=0}^n\frac{(-1)^{n-k}(k+1)^{k-1}k^{n-k}}{k!(n-k)!}x^n$

$\displaystyle =\sum_{k \ge 0}\frac{(-1)^k(k+1)^{k-1}k^{-k}}{k!}\sum_{n \ge k}\frac{(-kx)^n}{(n-k)!}=\sum_{k \ge 0}\frac{(-1)^k(k+1)^{k-1}k^{-k}}{k!}\sum_{n \ge 0}\frac{(-kx)^{n+k}}{n!}$

$\displaystyle =\sum_{k \ge 0}\frac{(k+1)^{k-1}x^k}{k!}\sum_{n \ge 0}\frac{(-kx)^n}{n!}=\sum_{k \ge 0}\frac{(k+1)^{k-1}x^k}{k!}e^{-kx}=\sum_{k \ge 0}\frac{(k+1)^{k-1}}{k!}(xe^{-x})^k$

$\displaystyle \begin{aligned}=\sum_{k \ge 0}\frac{(k+1)^k}{(k+1)!}(xe^{-x})^k=\sum_{k \ge 1}\frac{k^{k-1}}{k!}(xe^{-x})^{k-1}=-\frac{e^x}{x}\sum_{k \ge 1}\frac{(-k)^{k-1}}{k!}(-xe^{-x})^k=-\frac{e^x}{x}W_0(-xe^{-x}),\end{aligned}$

where $W_0$ is the Lambert function (see Problem 2 in this post for the Maclaurin series expansion of $W_0$ ). So since, by definition, $W_0(te^t)=t$ for $t \ge -1,$ we have $W_0(-xe^{-x})=-x$ and hence $f(x)=e^x,$ which gives

$\displaystyle \sum_{n \ge 0}\frac{a_n}{n!}x^n=f(x)=e^x=\sum_{n \ge 0}\frac{x^n}{n!}.$

Therefore $a_n=1,$ for all $n \ge 0,$ and the result follows. $\ \Box$

The Maclaurin series expansion of the function (1+x)(1+x/a)(1+x/a^2)(1+x/a^3) …

Problem. Show that

$\displaystyle \begin{aligned}f(x):=\prod_{n=0}^{\infty}\left(1+\frac{x}{a^n}\right)=1+\sum_{n=1}^\infty\frac{a^n}{\prod\limits_{k=1}^n(a^k-1)}x^n, \ \ \ \ \ a,x \in \mathbb{R}, \ \ \ |a| > 1.\end{aligned}$

Solution. Let

$\displaystyle f(x)=\sum_{n=0}^{\infty}c_nx^n.$

Notice that $c_0=f(0)=1.$ Now,

$\displaystyle \begin{aligned}\sum_{n=0}^{\infty}c_nx^n=f(x)=(1+x)\prod_{n=1}^{\infty}\left(1+\frac{x}{a^n}\right)=(1+x)\prod_{n=0}^{\infty}\left(1+\frac{x}{a^{n+1}}\right)=(1+x)\prod_{n=0}^{\infty}\left(1+\frac{x/a}{a^n}\right)\end{aligned}$

$\displaystyle =(1+x)f(x/a)=(1+x)\sum_{n=0}^{\infty}c_n(x/a)^n=(1+x)\sum_{n=0}^{\infty}\frac{c_n}{a^n}x^n$

$\displaystyle =\sum_{n=0}^{\infty}\frac{c_n}{a^n}x^n+\sum_{n=0}^{\infty}\frac{c_n}{a^n}x^{n+1}=\sum_{n=0}^{\infty}\frac{c_n}{a^n}x^n+\sum_{n=1}^{\infty}\frac{c_{n-1}}{a^{n-1}}x^n=1+\sum_{n=1}^{\infty}\frac{c_n+ac_{n-1}}{a^n}x^n$

and so

$\displaystyle c_n=\frac{c_n+ac_{n-1}}{a^n}, \ \ \ \ \ n \ge 1,$

which gives

$\displaystyle c_n=\frac{ac_{n-1}}{a^n-1}=\frac{a^2c_{n-2}}{(a^n-1)(a^{n-1}-1)}= \cdots =\frac{a^nc_0}{(a^n-1)(a^{n-1}-1) \cdots (a-1)}$

$\displaystyle =\frac{a^n}{(a^n-1)(a^{n-1}-1) \cdots (a-1)}=\frac{a^n}{\prod_{k=1}^n(a^k-1)}. \ \Box$

Convergence of an infinite series related to the sequence a_{n+1}=e^(-a_0-a_1- … -a_n)

The following was posted on AoPS last year; you can see the problem and my solution here. The first part of the solution I’m giving here is slightly more elementary.

Problem (American Mathematical Monthly). Consider the sequence $\{a_n\}$ defined by

$\displaystyle a_0 > 0, \ \ \ \ a_{n+1}=e^{-(a_0+a_1+ \cdots + a_n)}, \ \ \ \ n \ge 0.$

For which values of $b$ does the series $\displaystyle \sum_{n=0}^{\infty}a_n^b$ converge?

Solution (Y. Sharifi). Since $a_0 > 0,$ it’s clear that $a_n > 0$ for all $n \ge 0,$ and hence either $\displaystyle S:=\sum_{n=0}^{\infty} a_n$ converges or $S=\infty.$ If $S$ converges, then $\displaystyle \lim_{n\to\infty}a_n=0$ and if $S=\infty,$ then

$\displaystyle \begin{aligned}\lim_{n\to\infty}a_n=\lim_{n\to\infty}\exp\left(-\sum_{k=0}^{n-1}a_k\right)=\exp\left(-\lim_{n\to\infty}\sum_{k=0}^{n-1}a_k\right)=\exp(-S)=0.\end{aligned}$

So either way, $\displaystyle \lim_{n\to\infty}a_n=0.$ Also notice that

$\displaystyle a_{n+1}= e^{-a_0- \cdots -a_{n-1}}e^{-a_n}=e^{-(a_0+a_1+ \cdots + a_{n-1})}e^{-a_n}=a_ne^{-a_n}.$

So, by Stolz–Cesàro,

$\displaystyle \begin{aligned}\lim_{n\to\infty}\frac{1}{na_n}=\lim_{n\to\infty}\left(\frac{1}{a_{n+1}}-\frac{1}{a_n}\right)=\lim_{n\to\infty}\left(\frac{1}{a_ne^{-a_n}}-\frac{1}{a_n}\right)=\lim_{n\to\infty}\frac{e^{a_n}-1}{a_n}=\lim_{x\to0}\frac{e^x-1}{x}=1.\end{aligned}$

Hence $\displaystyle \lim_{n\to\infty}na_n=1$ and so, by the limit comparison test, $\displaystyle \sum a_n^b$ converges if and only if $\displaystyle \sum \frac{1}{n^b}$ converges. Thus the answer is all the real numbers $b > 1. \ \Box$

Intermediate points in mean value theorem (2)

Problem. Let $f: [a,b] \to [0,\infty)$ be a continuous and strictly increasing function. By the mean value theorem for integrals, for every $x > 0$ there exists (a unique) $c_x \in (a,b)$ such that $\displaystyle \int_a^b(f(t))^xdt=(b-a)(f(c_x))^x.$ Show that $\displaystyle \lim_{x\to\infty}c_x=b.$

Solution. We have

$\displaystyle \lim_{x\to\infty}f(c_x)=\lim_{x\to\infty}\left(\frac{1}{b-a}\int_a^b(f(t))^x \ dt\right)^{1/x}=\lim_{x\to\infty}\left(\int_a^b(f(t))^x \ dt\right)^{1/x}$

and hence, by this post,

$\displaystyle \lim_{x\to\infty}f(c_x) =\max_{t\in[a,b]}f(t)=f(b). \ \ \ \ \ \ \ \ \ \ (*)$

Since $f$ is continuous and increasing, $f^{-1}$ exists and is continuous. Thus, by $(*),$

$\displaystyle \lim_{x\to\infty}c_x=\lim_{x\to\infty}f^{-1}(f(c_x))=f^{-1}(\lim_{x\to\infty}f(c_x))=f^{-1}(f(b))=b. \ \Box$

A sequence of rational numbers converging to π/4

The following seems to be a Russian olympiad problem; it was posted on AoPS a couple of years ago; you can see the problem and my solution here.

Problem. Consider the sequences $\{p_n\}, \{q_n\}, \ n \ge -1,$ defined by

$p_{-1}=0 , \ \ p_0=1, \ \ \ \ \ p_n=2p_{n-1}+(2n-1)^2p_{n-2}, \ \ \ \ \ n \ge 1,$

$q_{-1}=q_0=1, \ \ \ \ \ \ \ \ q_n=2q_{n-1}+(2n-1)^2q_{n-2}, \ \ \ \ \ n \ge 1.$

Show that $\displaystyle \lim_{n\to\infty}\frac{p_n}{q_n}=\frac{\pi}{4}.$

Solution. We first find an explicit formula for $q_n.$

Claim 1. $\displaystyle q_n=\prod_{k=0}^n(2k+1),$ for all $n \ge 0.$

Proof. By induction over $n.$ We have $q_0=1, \ q_1=3=1 \times 3$ and, assuming $n \ge 2$ and the claim is true for all $0 \le m < n,$ we have

$\displaystyle q_n=2q_{n-1}+(2n-1)^2q_{n-2}=2\prod_{k=0}^{n-1}(2k+1)+(2n-1)^2\prod_{k=0}^{n-2}(2k+1)$

$\displaystyle =(2(2n-1)+(2n-1)^2)\prod_{k=0}^{n-2}(2k+1)=(4n^2-1) \prod_{k=0}^{n-2}(2k+1)$

$\displaystyle =(2n+1)(2n-1)\prod_{k=0}^{n-2}(2k+1)=\prod_{k=0}^n(2k+1).$

Claim 2. $\displaystyle p_nq_{n-1}-p_{n-1}q_n=(-1)^n\prod_{k=0}^{n-1}(2k+1)^2,$ for all $n \ge 1.$

Proof. Let $x_n:=p_nq_{n-1}-p_{n-1}q_n.$ Then $x_1=-1$ and since, as the problem has given us,

$\displaystyle p_n=2p_{n-1}+(2n-1)^2p_{n-2}, \ \ \ \ q_n=2q_{n-1}+(2n-1)^2q_{n-2},$

we have

$\displaystyle x_n=(2p_{n-1}+(2n-1)^2p_{n-2})q_{n-1}-p_{n-1}(2q_{n-1}+(2n-1)^2q_{n-2})$

$\displaystyle =-(2n-1)^2(p_{n-1}q_{n-2}-p_{n-2}q_{n-1})=-(2n-1)^2x_{n-1}$

and the claim follows.

Now, using the two claims, we can solve the problem. We have

$\displaystyle \frac{p_n}{q_n}=\frac{p_0}{q_0}+\sum_{m=1}^n\left(\frac{p_m}{q_m}-\frac{p_{m-1}}{q_{m-1}}\right)=1+\sum_{m=1}^n\frac{p_mq_{m-1}-p_{m-1}q_m}{q_mq_{m-1}}$

$\displaystyle \begin{aligned}=1+\sum_{m=1}^n\frac{(-1)^m\prod_{k=0}^{m-1}(2k+1)^2}{\prod_{k=0}^m(2k+1)\prod_{k=0}^{m-1}(2k+1)}=1+\sum_{m=1}^n\frac{(-1)^m}{2m+1}=\sum_{m=0}^n\frac{(-1)^m}{2m+1}\end{aligned}$

and so

$\displaystyle \lim_{n\to\infty}\frac{p_n}{q_n}=\lim_{n\to\infty} \sum_{m=0}^n\frac{(-1)^m}{2m+1}=\sum_{m=0}^{\infty}\frac{(-1)^m}{2m+1}=\tan^{-1}(1)=\frac{\pi}{4}. \ \Box$